My son received a Lego set as a Christmas gift. It contains a little policeman holding a black stick. An interesting question came to my mind. Can the black stick reach any point in the 3D world? Of course, the answer is NO. The toy only has two joints, shoulder and wrist, that can rotate 360 degree on two perpendicular planes. This means it is only able to reach points on a sphere. So how can we design an arm that is able to reach any point in the 3D world? We need to make both the arm and the black stick to be stretchable to arbitrary length. However, this seems that we have more degree freedom (4 DOF) than we need. If we set the arm to be a fixed length but not 0, then there are definitely some areas non-reachable.

Suppose we have this 4 DOF arm, how to control the arm to reach a point in 3D world? This is a little bit different from most existing arms. Most existing arms have more joints but no stretchable arms. In addition, in most cases they care about the gripper pose when grab things. Anyway, here we have a simplified problem. To be honest, I have never worked on a robot arm before. However, as a SLAMer, I am familiar with coordinates transformation and non-linear optimization. So I formulated it as an optimization problem and wrote a simple simulator/solver in python. As shown in the figure below, $g$ is the goal position, and $f(\theta_1, \theta_2. r_1, r_2) = ^0P$ is the position of the end effector

You will run into singularity issues if using Gauss Newton. So I am using a Levenberg Marquardt-ish solver. What surprised me is that the solver can always find a solution for 10000 random trials. I thought it might run into a local minimum if the initial position is far from the goal position in such a nonlinear optimization problem.

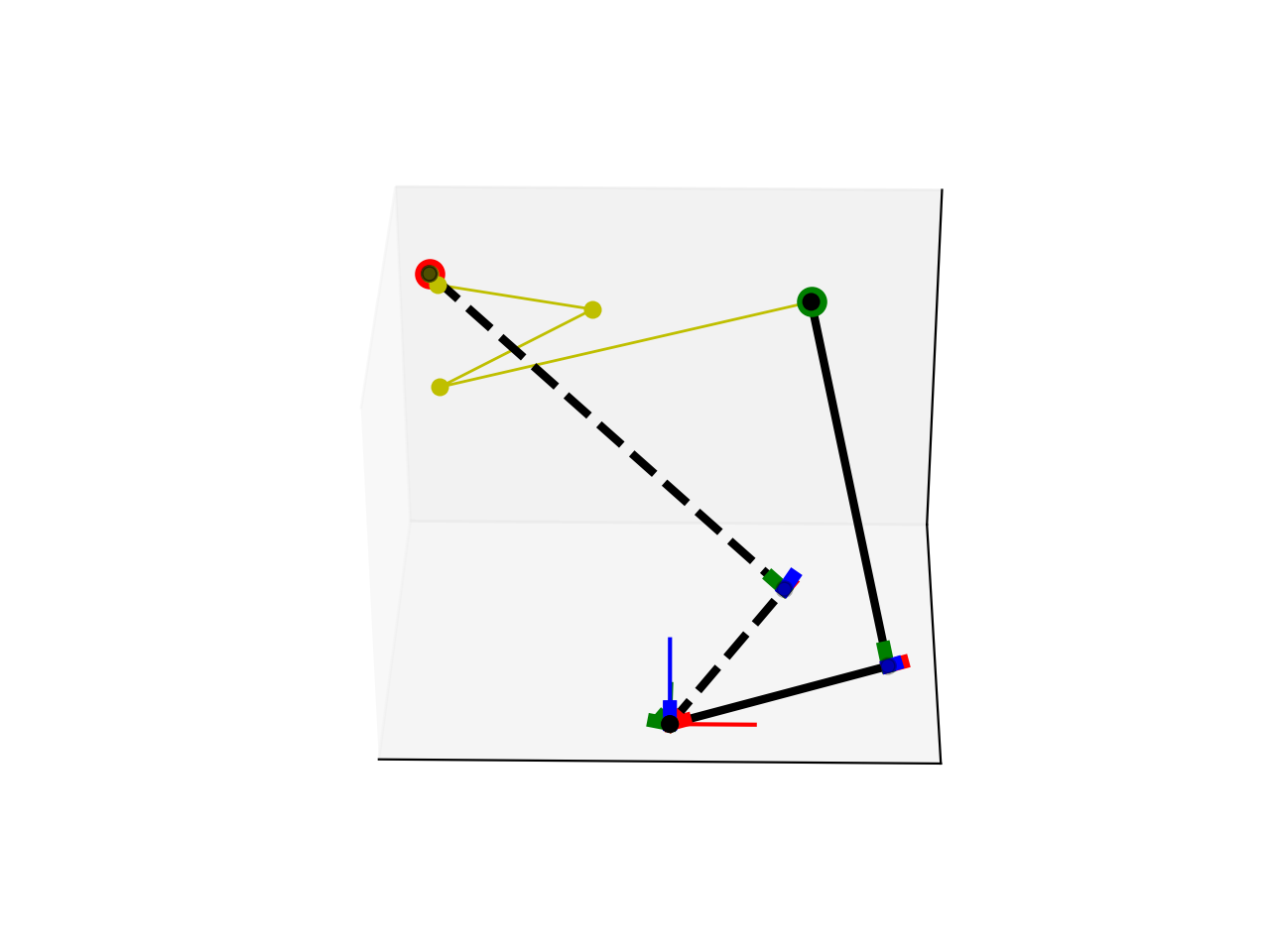
However, without constraining the velocity, you can see huge jumps. So I set some constraints on the size of the update step. Though we spend more iterations to reach the goal, the trajectory is still not very smooth. If we control the arm to set the joint angle one by one, this might not be a problem. Actually, I am not sure how a real arm is controlled. Do we directly set the joint angle or control the angular velocity?

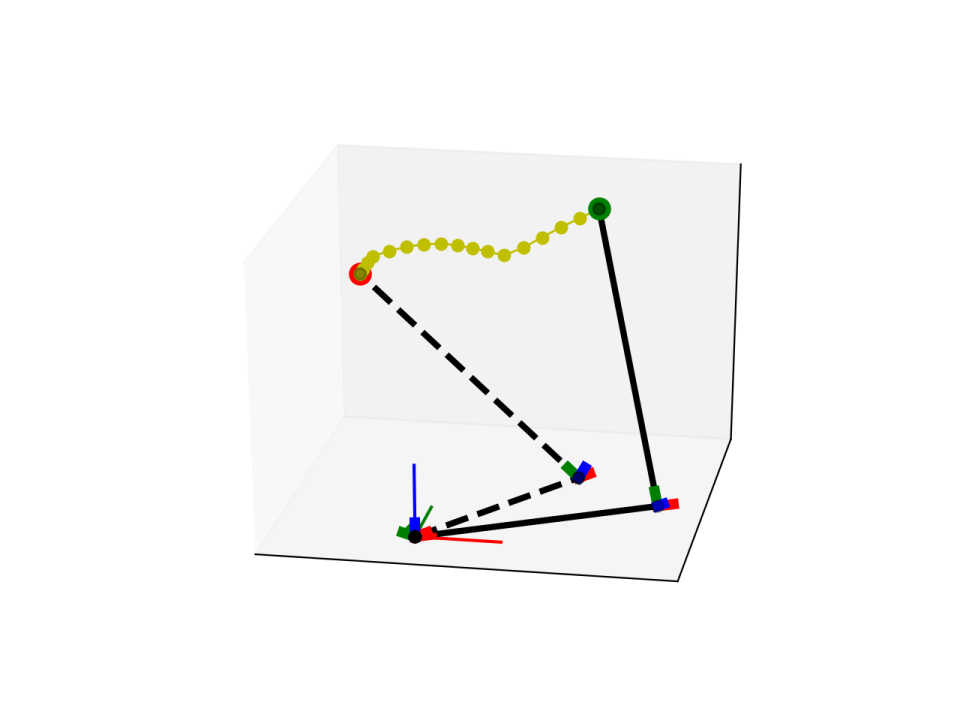
Anyway, I am really curious about the convergence property. Why can it always find a solution? In order to have a better/easier visualization, I tried a different configuration which only has 2 DOF (2 joints, fixed arm and stick length). Interestingly, if there are solutions (the goal point should lie on the same sphere of the initial position), the solver can always find a solution. After I see a plot of a cost surface for a test case shown below, I was shocked that though there are several local minimums, they are also global minimums.

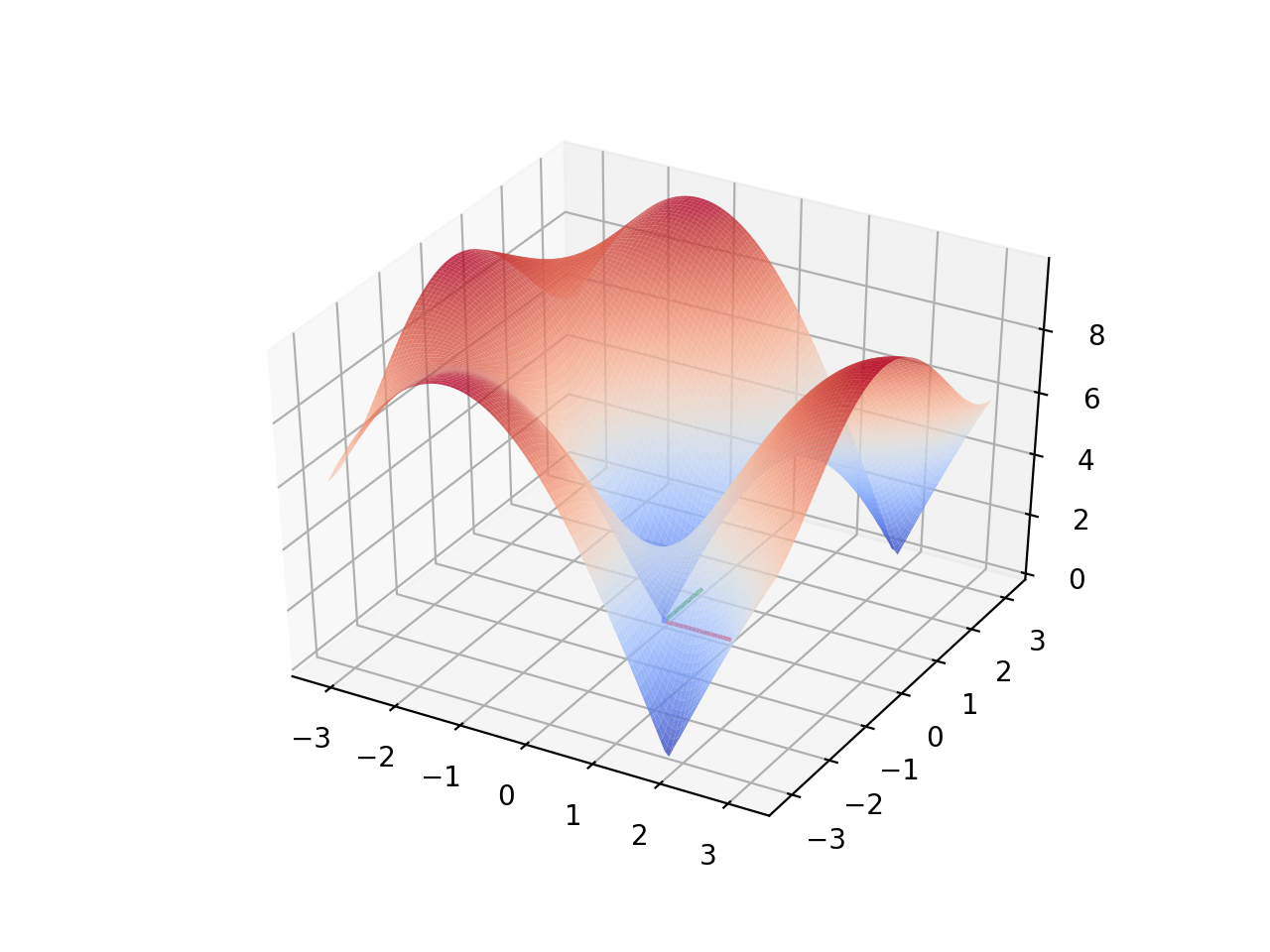
Interesting! I haven’t proved it why this happens. But if the solver can always converge to a correct solution in the 2 DOF case, I think I found a way to solve the 4 DOF case. As we know that the goal position must satisfy $x^2 + y^2 + z^2 = r1^2 + r2^2$, I can first change the lengths of the arm and the stick to satisfy the constraint, and then let the solver find the solution of the angles of two joints. In addition to guaranteed convergence, the arm trajectory is predictable and is smoother than the one generated by using LM without leveraging geometry information.

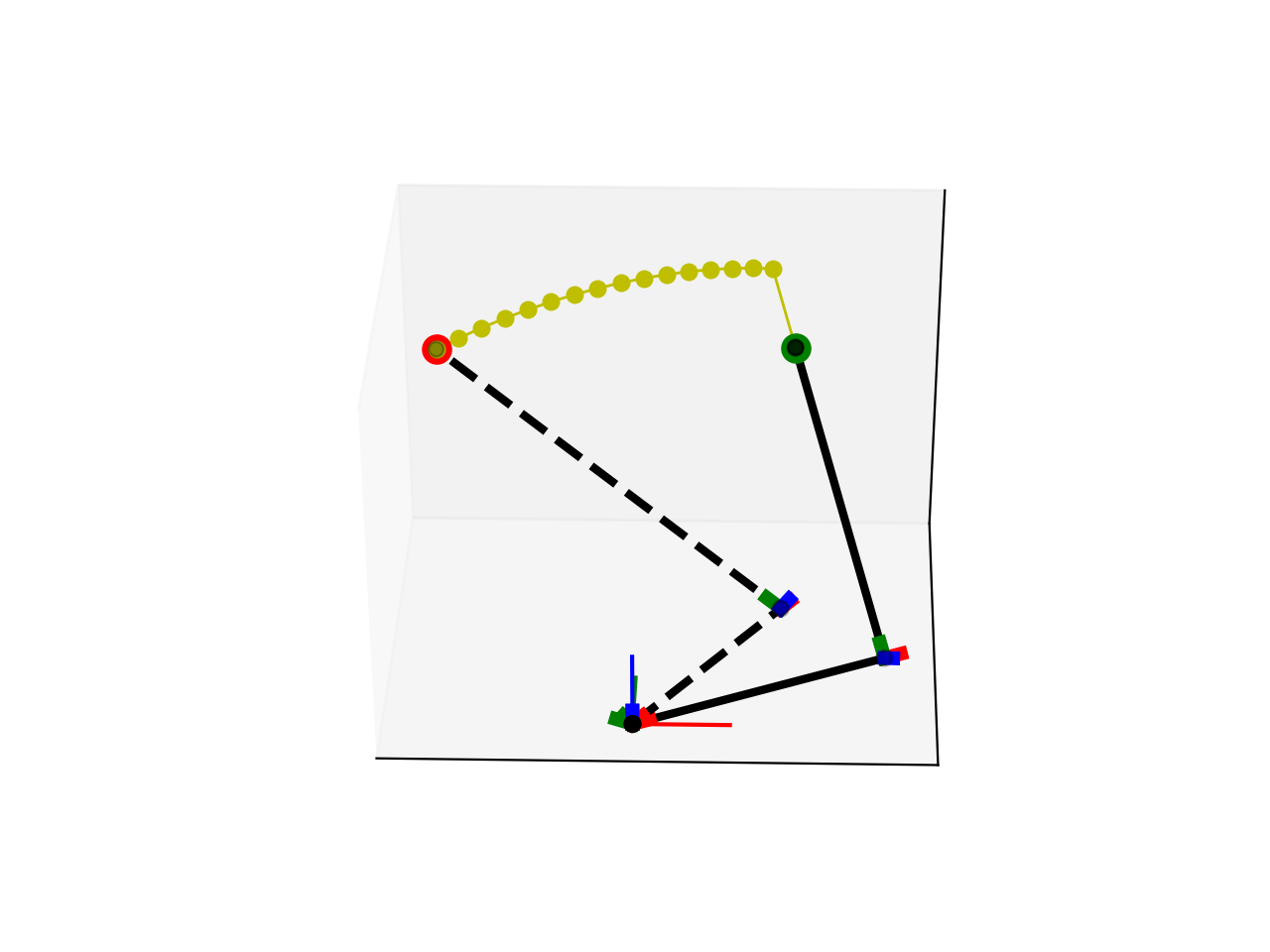
Though this is very simple or maybe other people have found this long time ago, as my first robot arm project, I had lots of fun on my last day hacking in 2020. :)

Code is here.