I have two functions $f1(x, y) = x^2 + y^2$ and $f2(x, y) = x^2 + 10 * y^2$. It is very easy to calculate their gradients and hessian matrices.

\[H1 = \begin{bmatrix} 2, 0 \\0, 2 \end{bmatrix},\ cond(H1) = 1 \\ H2 = \begin{bmatrix} 2, 0 \\0, 20 \end{bmatrix},\ cond(H2) = 10 \\\]

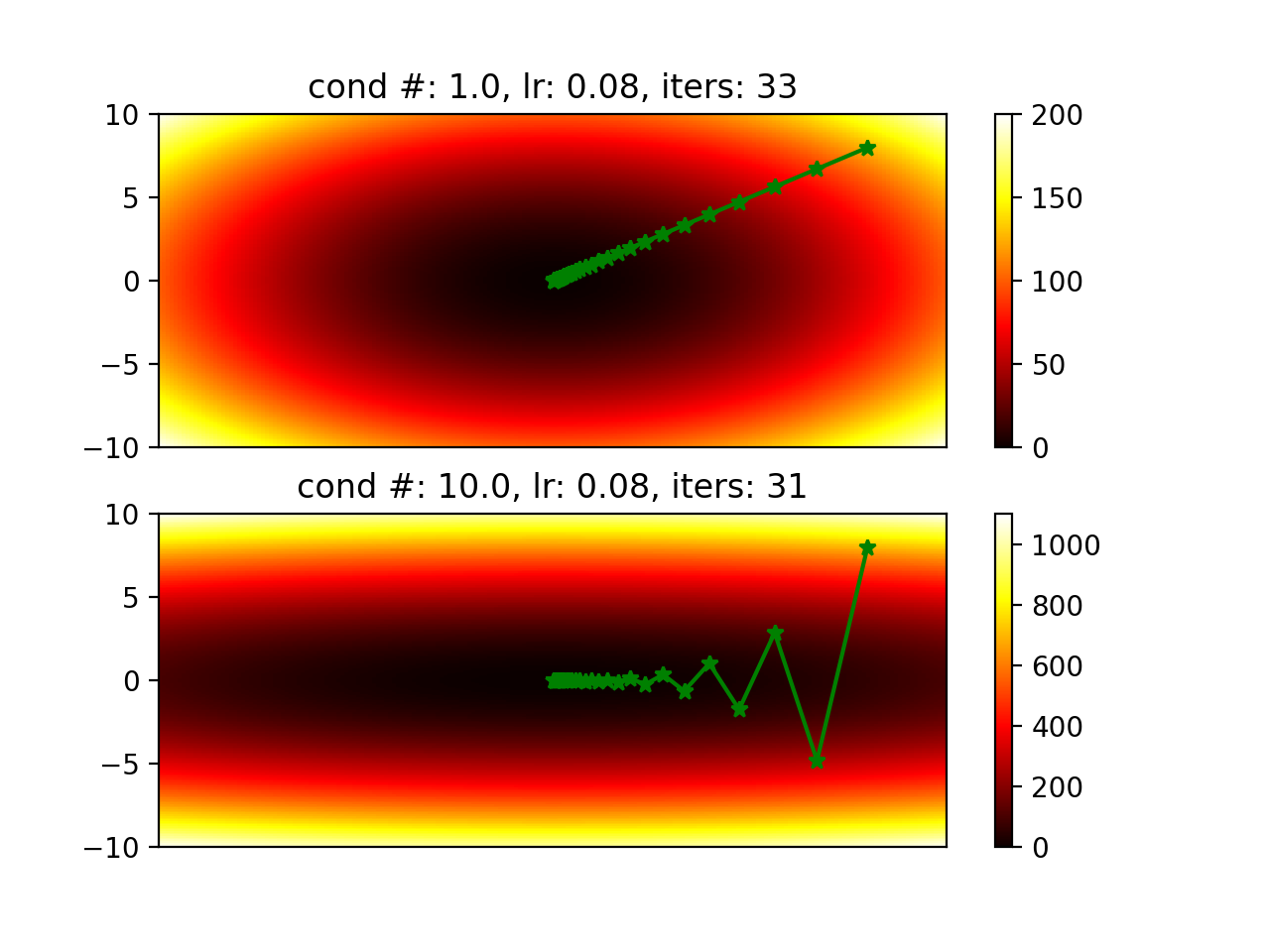
We often see the figure below and hear that it converges slower with a hessian matrix that has a larger condition number.

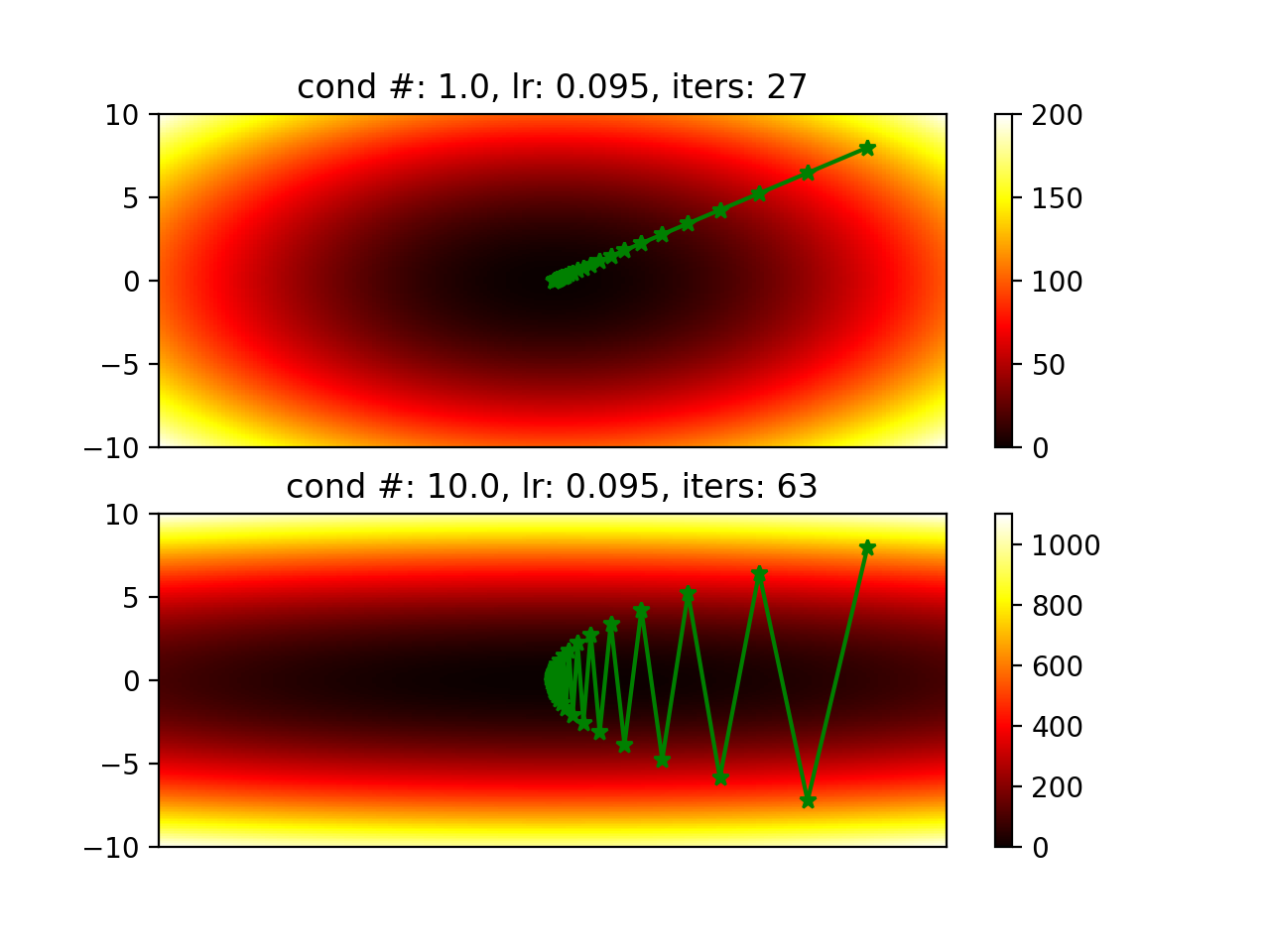
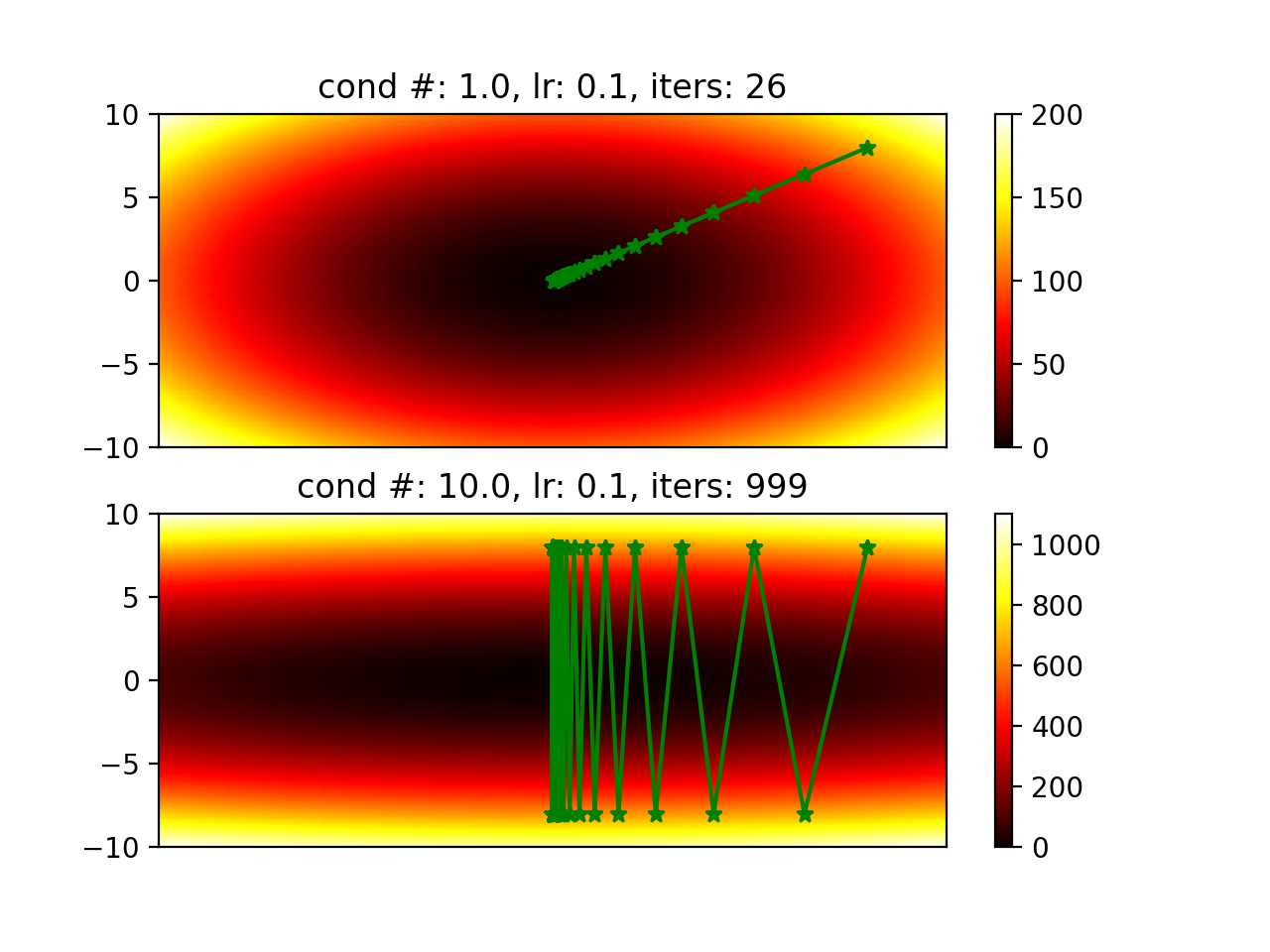
Will it always converge slower when its hessian has a larger condition number? It actually depends on the learning rate. Figures below are generated by changing learning rate.

• I think with a smaller condition number, we can try to use a larger learning rate to make it converge faster. When condition number is very large, it means the magnitude of one direction of the gradient is much smaller than another one. Then if you try a large learning rate, it is more likely to overshoot in one direction.

• Normalize data to make x, y, … into similar range so we can have hessians with smaller condition number.

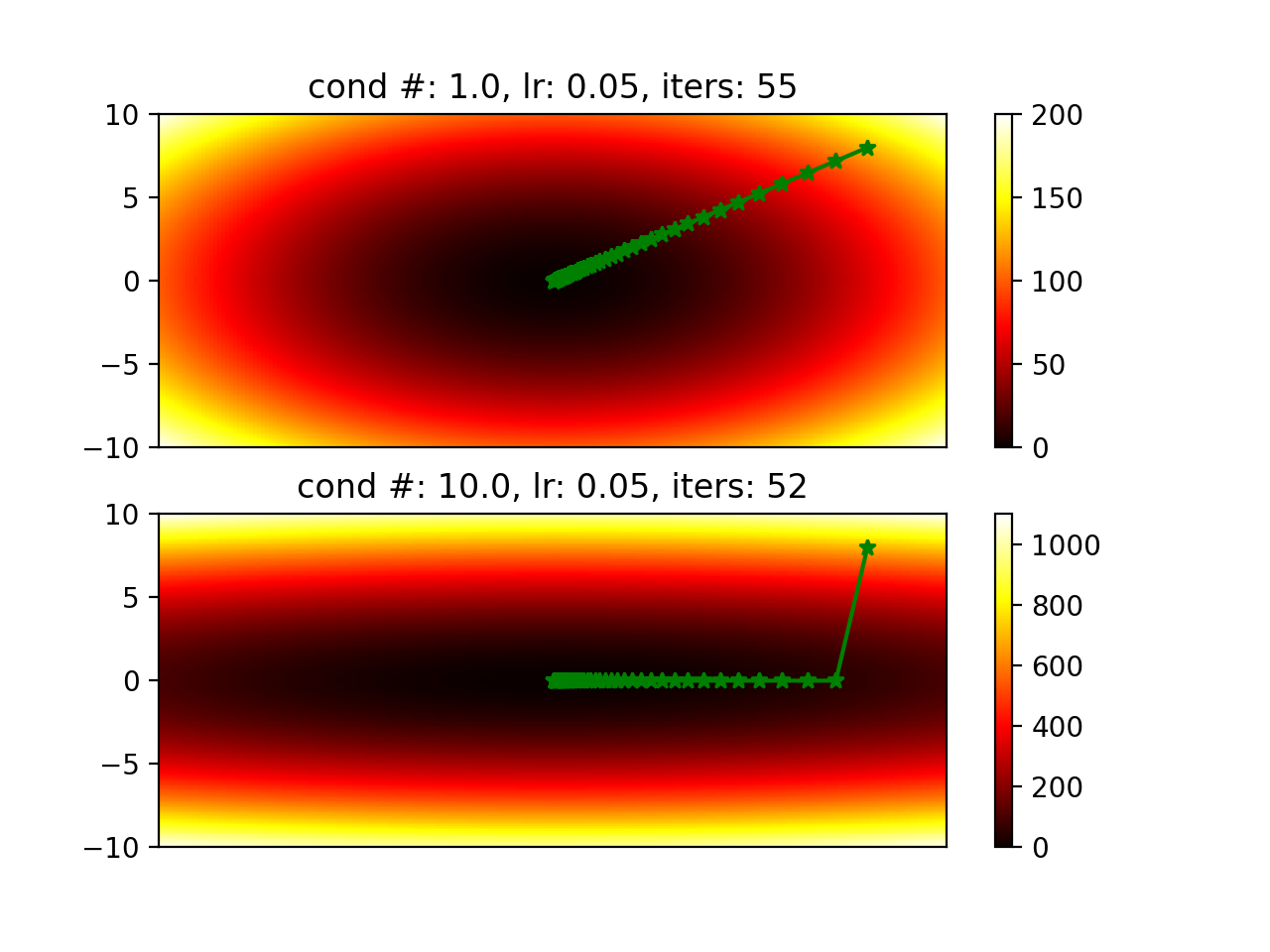
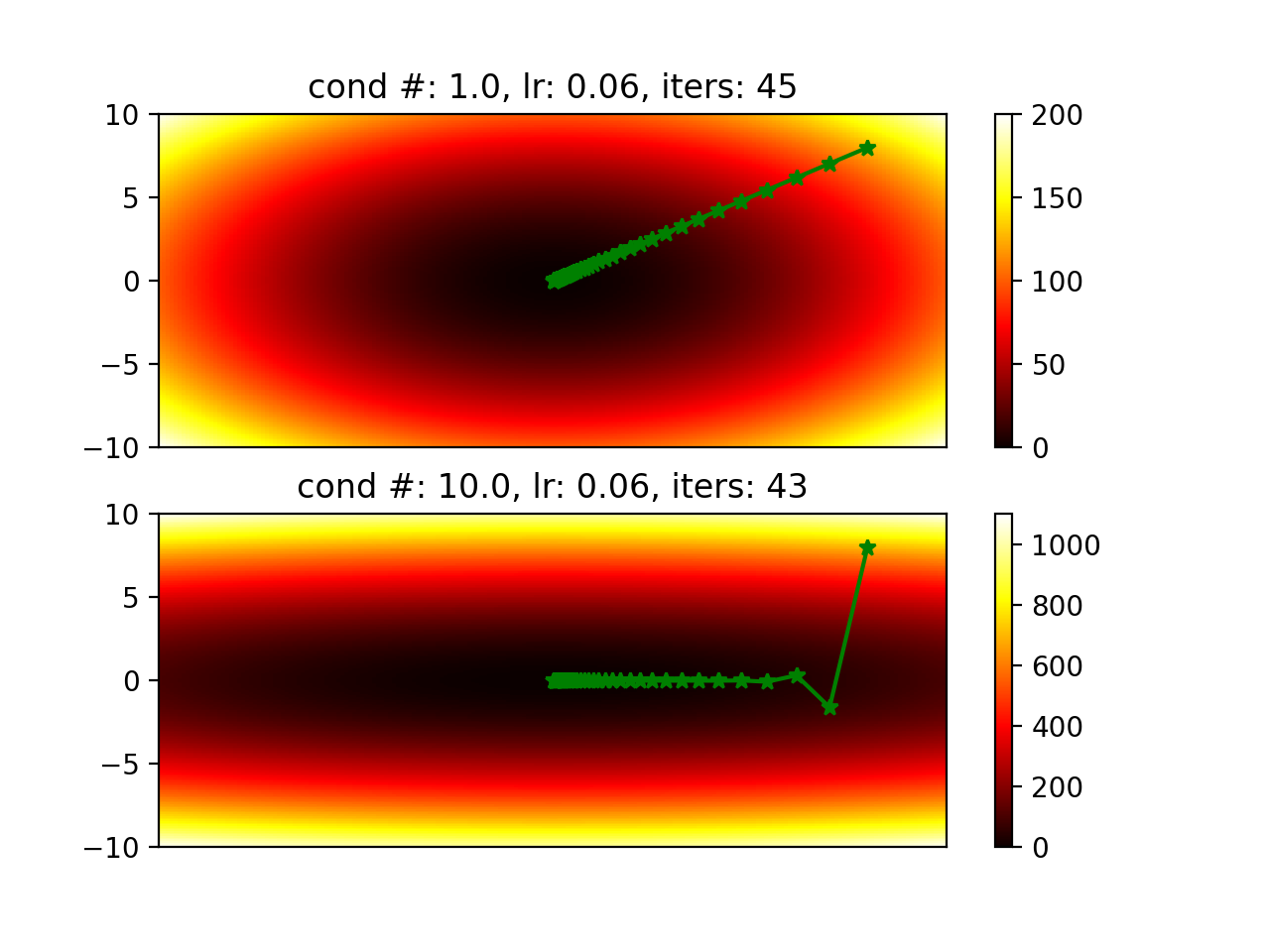
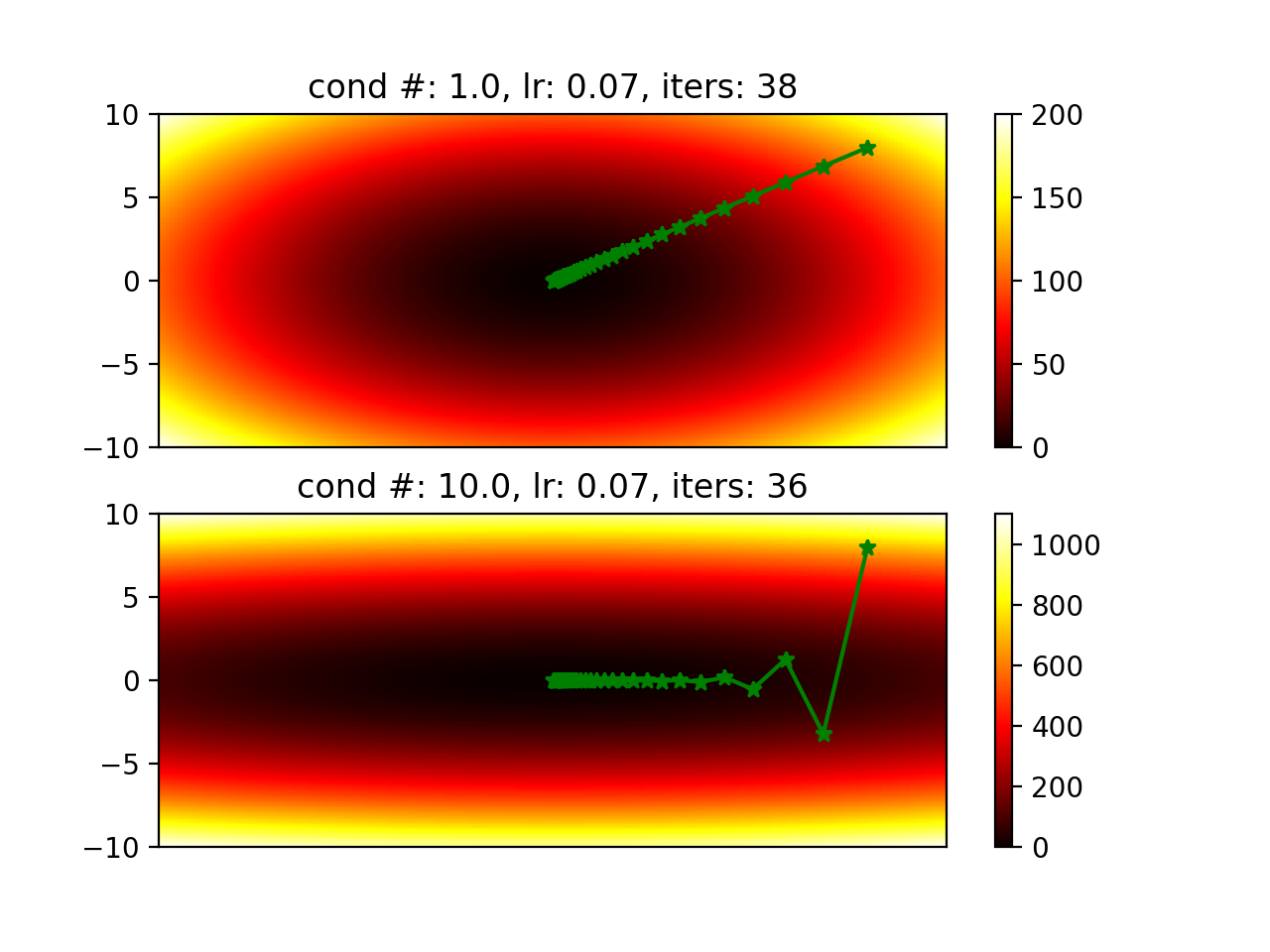
Code is here

part 2: Gaussian newton, adagrad

Gradient descent is $x -= \lambda * g$, where $g$ is the gradients. A basic Adagrad is $x -= \lambda * \frac{g}{g^2}$, where $g^2$ is element-wise operation. How does this relate to Newton method or Gauss-Newton method? I think it is kind of using preconditioners.

Netwon method is like $x -= H^{-1}g$. Gauss-Netwon is like $x -= (gg^T)^{-1}g$ ($g$ is gradient which is the transpose of Jacobian matrix $J^T$ since target function is a scalar). Calculating inverse of hessian $H^{-1}$ or $(gg^T)^{-1}$ is time consuming. So we can choose a preconditioner to replace them such as only using diagonal elements in $gg^T$.