One of most useful things I learned in graduate school is max-heap. It can be applied to many scenarios where you need to find a target with minimal cost. In this post, I will explain a DFS-based clothoid planner.

I am definitely not an expert on planning/control stuff. But I always find it is interesting to view it as an optimization problem. If you are also new to planning/control, let me first introduce you two very simple but elegant planning/control algorithms.

The first one is dynamic-window based. I used it in my PhD thesis when I needed to build a simulator for diff-drive mobile robots.

The second one is called dubins path planner. It will blow your mind if you never heard of it before.

One drawback of dubins though is that it is not very straightforward to incorporate obstacle avoidance since the planning algorithm only breaks the path into three parts - turn, straight, then turn without considering the obstacles in the path. So how can we find a path for a bicycle mode?

First, we need to know how to control a bicycle. As shown in the figure below, given steering angle $\alpha$ and linear velocity $v$, we can find the linear and angular velocity of the back wheel of the vehicle.

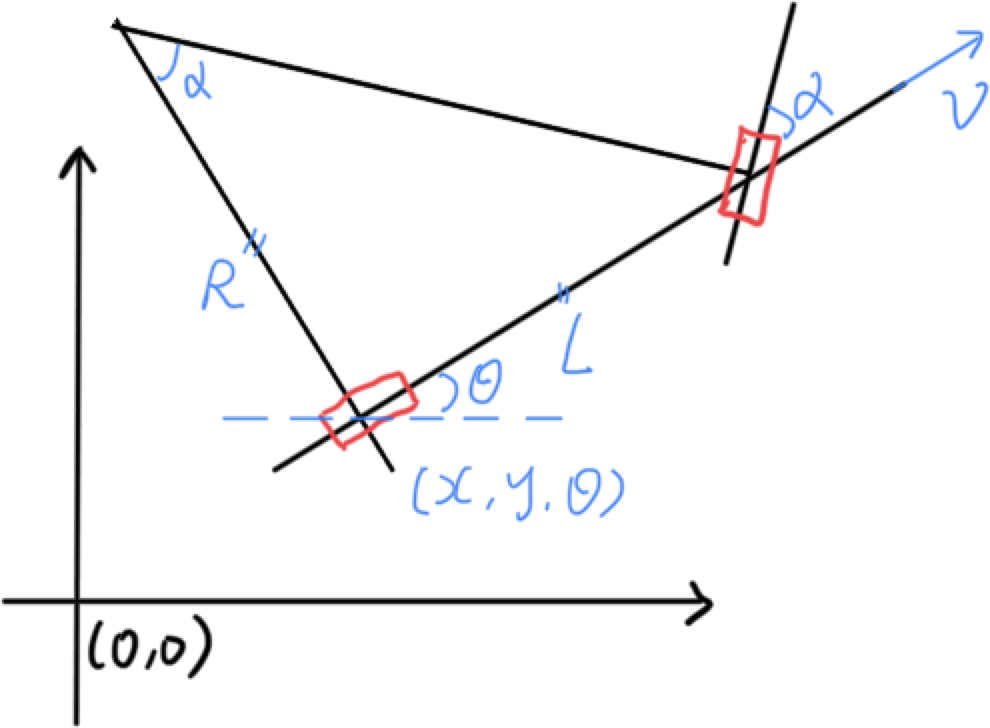
\[R = \frac{L}{tan(\alpha)}\] \[\dot{x} = vcos(\theta)\] \[\dot{y} = vsin(\theta)\] \[\dot{\theta} = \omega = \frac{v}{R}\]

Now, let’s assume the vehicle is moving at a constant low speed (we love low speed!). Then given a time horizon and steering angle, we can simulate how the vehicle moves. However, if you set a fixed steering angle, the vehicle will either go straight or move on a circle. Here comes clothoid. Instead of simulating a fixed steering angle, we will simulate a starting steering angle and an ending steering angle. Since the steering can only change continuously, the vehicle will travel on a clothoid (spiral).

Now comes the tree search. Each node represents a forward simulated state. The branches stop expanding when some nodes run into obstacles or reach the goal. The path from the base node to a leaf node represents a successful path. Now, we just need to define a cost to select the best one.

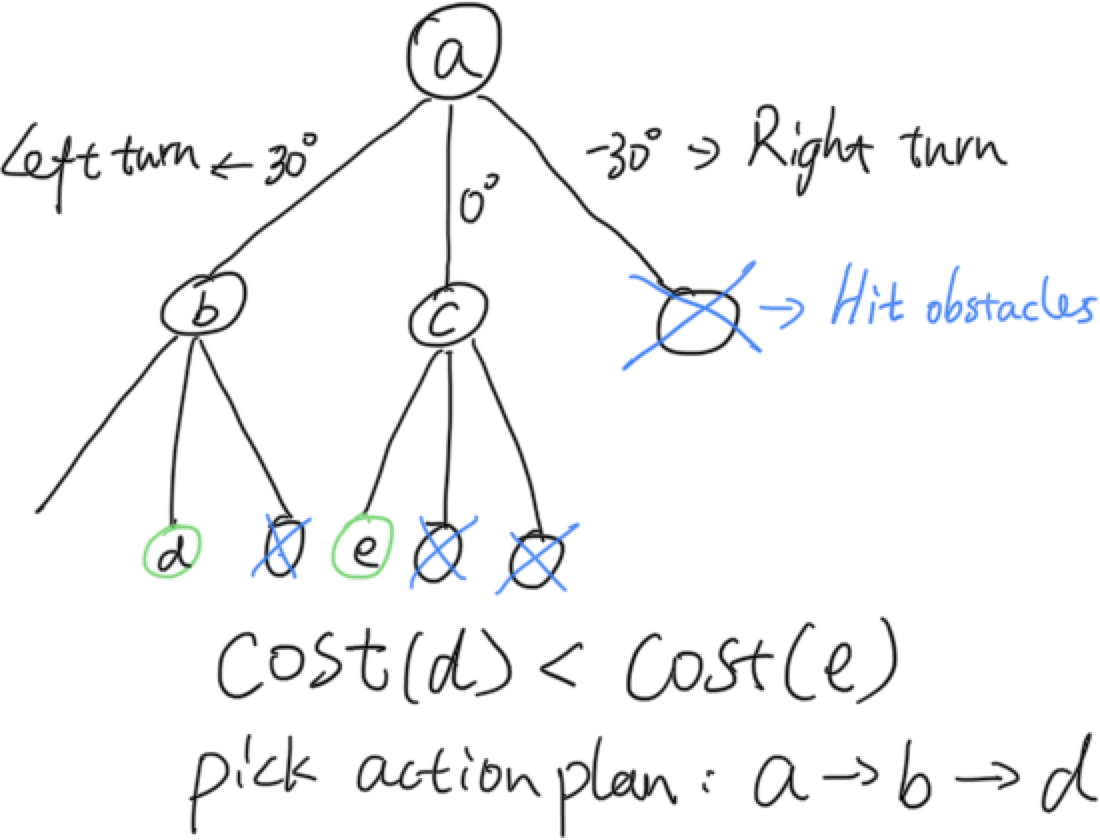
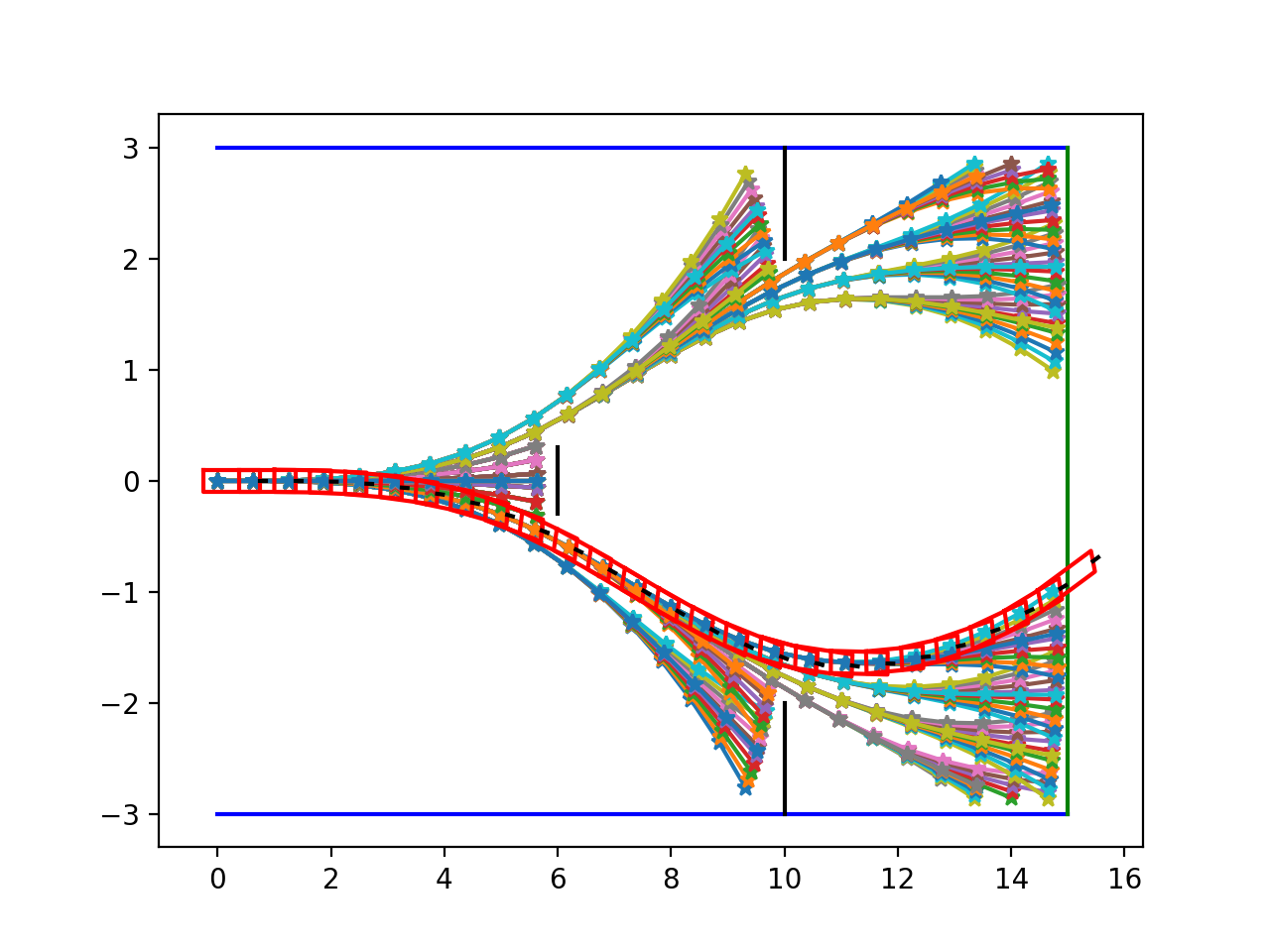
One way is trying to make the vehicle follow the central line. Another one could be keeping the vehicle aways from both boundaries as far as possible. As shown in the figure below, there are thousands of possible paths, but we finally pick the one in which the vehicle goes straight.

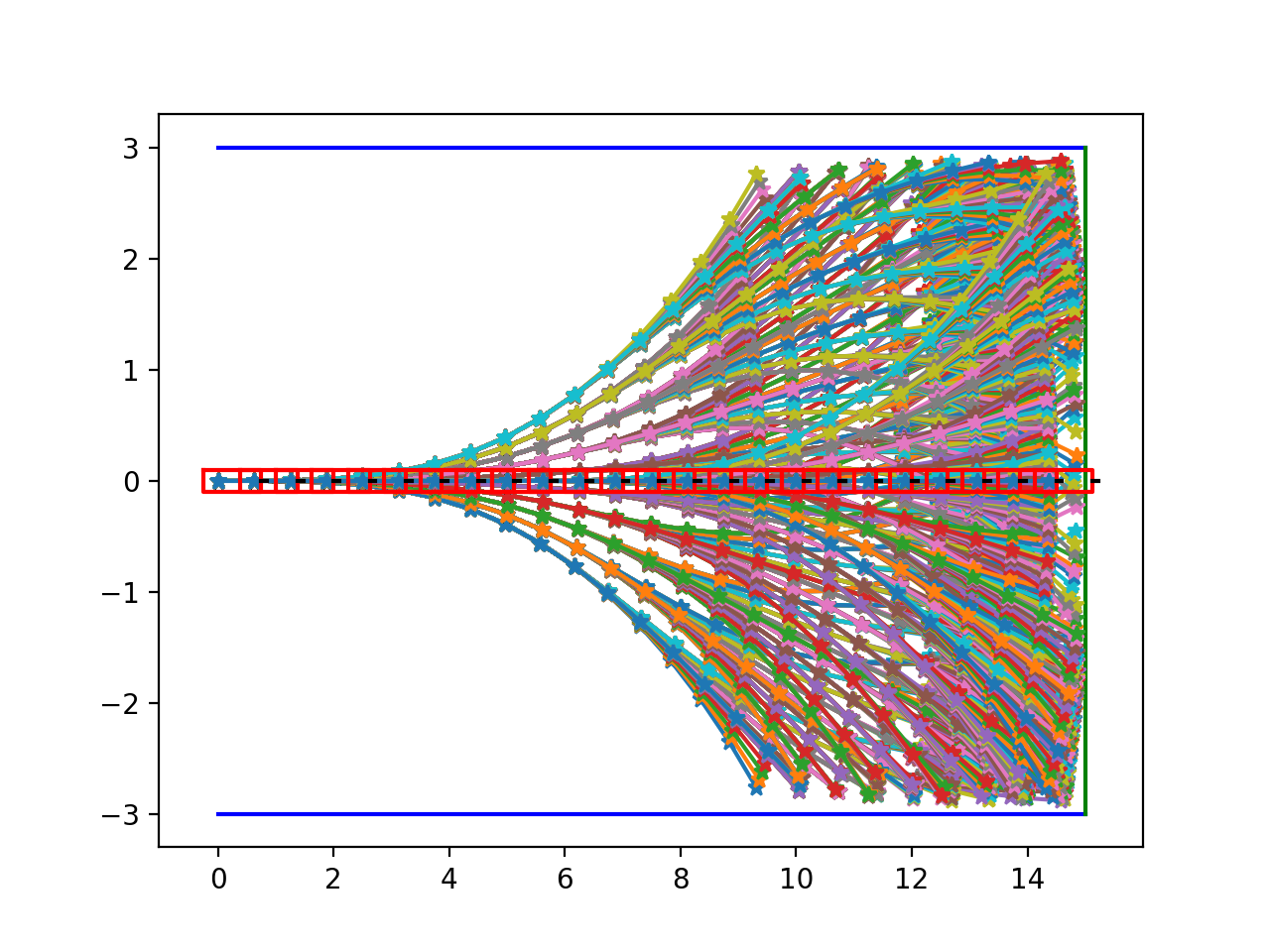
When there are obstacles, we can easily eliminate trajectories run into them.

The figures above only show the planned path at the start point. In reality, since the vehicle will not move perfectly along the path and there are dynamic obstacles, the vehicle needs to do re-planning frequently. This becomes challenging when the vehicle moves at a very high speed. So that’s why we love low speed!

So in my opinion, this is one way of solving a planning problem: 1. Get the model 2. Do the forward simulation 3. Pick the best one (with low speed profile if it is Okay). What’s an alternative way? Similar to the arm planning problem in one of my posts, we can solve it using Guass-Newton optimization (Or you may say inverse kinematics). But then, how can we incorporate obstacle avoidance? :)

As usual, code is here