• Motivation
  • – Robot Arm Control (Non-linear Least Square)
  • – Line Fitting (Linear Least Square)
• Gauss–Newton
  • – Gradient
  • – Jacobian Matrix
  • – Gauss-Newton Algorithm

Motivation

– Robot Arm Control (Non-linear Least Square)

• Robot Arm Control Example

– Line Fitting (Linear Least Square)

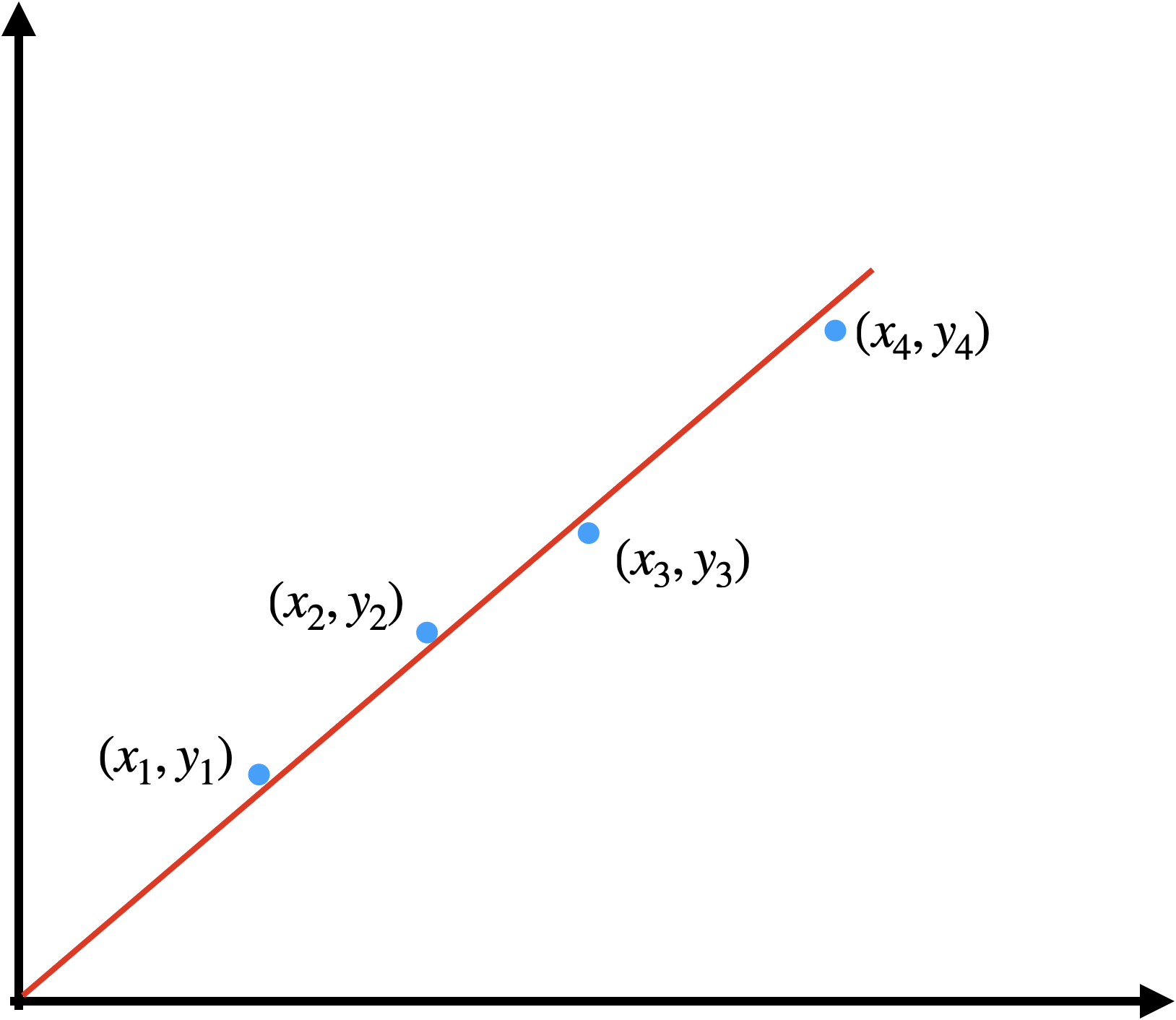
\[\textbf{x} = \underset{\alpha,\ \beta \in \mathbb{R}^n}{\operatorname{argmin}}(\|\alpha x_1 + \beta - y_1\|^2 + \|\alpha x_2 + \beta - y_2\|^2 + \|\alpha x_3 + \beta - y_3 \|^2 + \|\alpha x_4 + \beta - y_4\|^2) \\ = \underset{\alpha,\ \beta \in \mathbb{R}^n}{\operatorname{argmin}}( (\begin{bmatrix} x_1, 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_1)^T(\begin{bmatrix} x_1, 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_1) + (\begin{bmatrix} x_2, 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_2)^T(\begin{bmatrix} x_2, 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_2) \\ + (\begin{bmatrix} x_3, 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_3)^T(\begin{bmatrix} x_3, 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_3) + (\begin{bmatrix} x_4, 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_4)^T(\begin{bmatrix} x_4, 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} - y_4) ) \\ = \underset{\alpha,\ \beta \in \mathbb{R}^n}{\operatorname{argmin}}( (\begin{bmatrix} x_1, 1 \\ x_2, 1 \\ x_3, 1 \\ x_4, 1\end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{bmatrix})^T (\begin{bmatrix} x_1, 1 \\ x_2, 1 \\ x_3, 1 \\ x_4, 1\end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} - \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{bmatrix}) ) \\ = \underset{\alpha,\ \beta \in \mathbb{R}^n}{\operatorname{argmin}}(\|A\begin{bmatrix} \alpha \\ \beta\end{bmatrix} - b\|^2)\]

Check Pseudo Inverse in Linear algebra to solve the minimization problem above.

Gauss–Newton

– Gradient

– Jacobian Matrix

– Gauss-Newton Algorithm