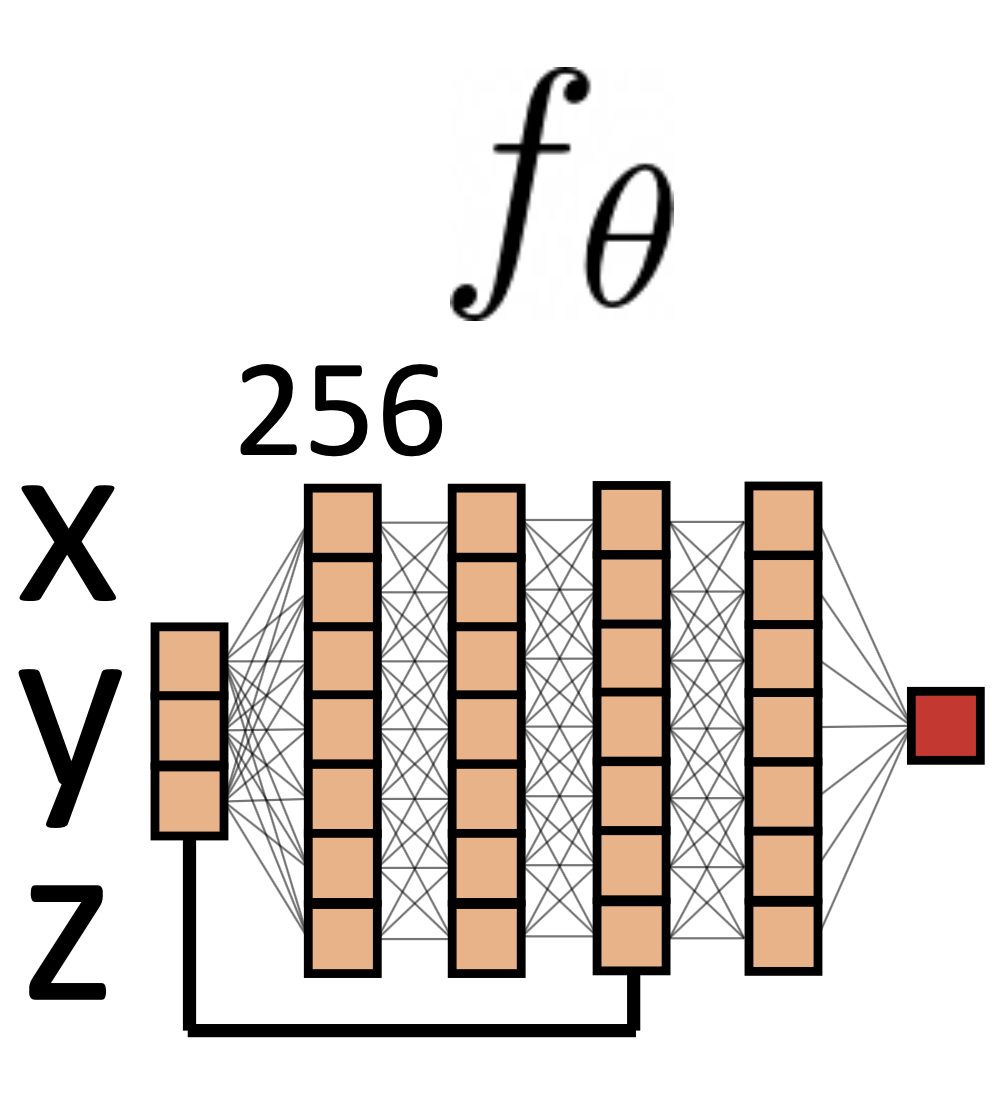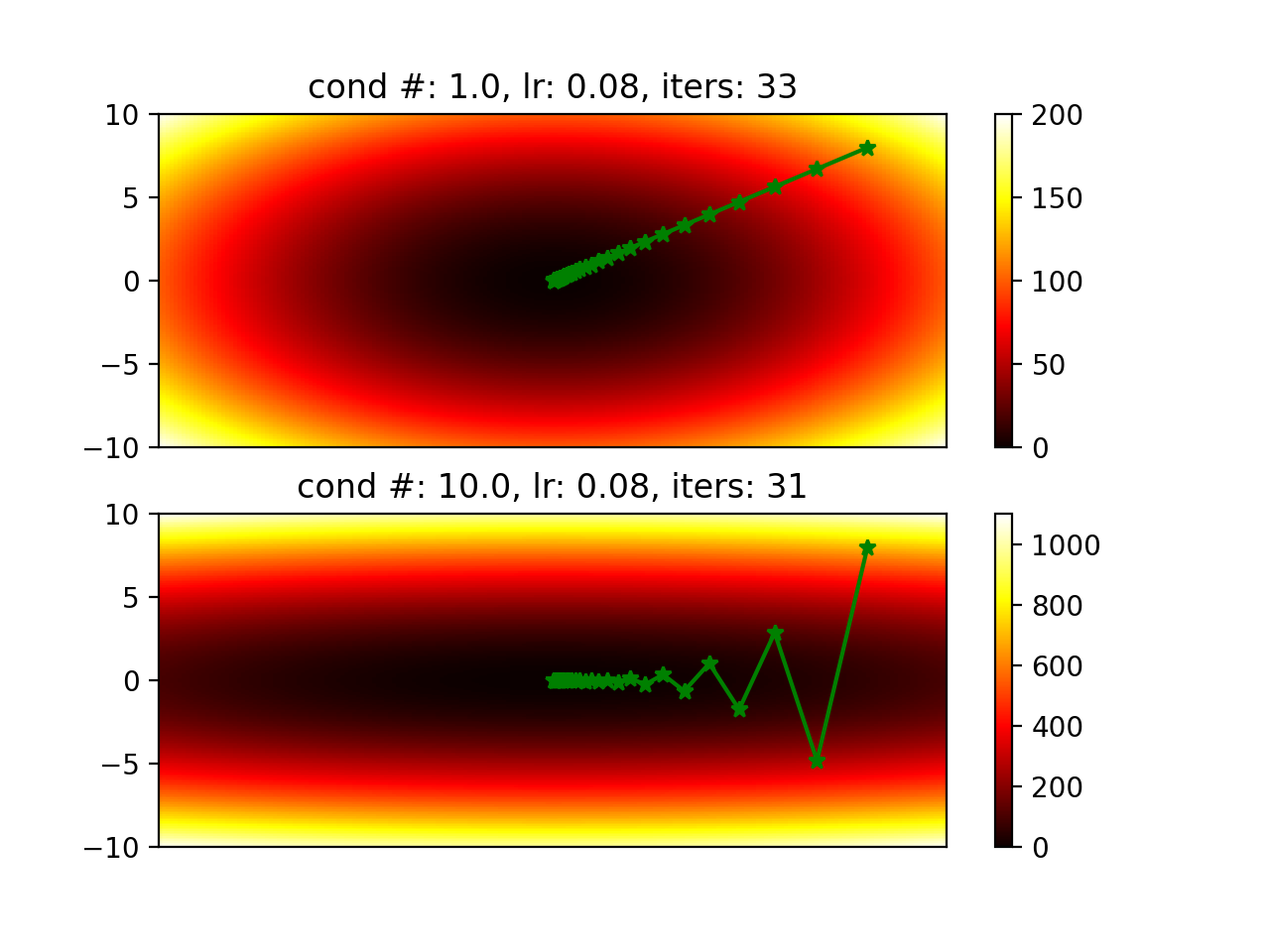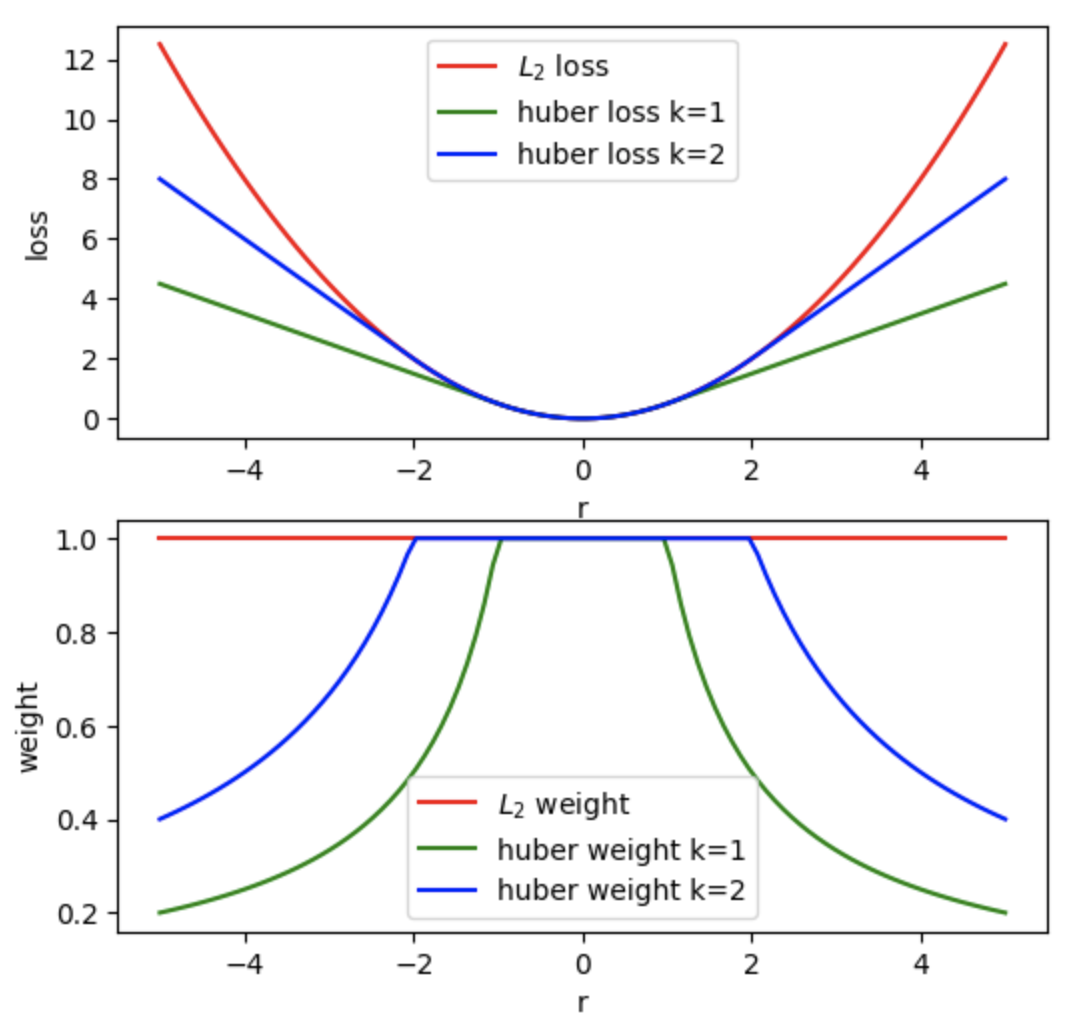
Robust Loss Functions for Least Square Optimization
In most robotics applications, maximizing posterior distribution is converted into a least square problem under the assumption that residuals follow Gaussian distribution. However, errors are not Gaussian distributed in practice. This makes the naive least square formulation not very robust to outliers with large residuals. In this post, we will first explore robust kernel approachs, then try to model residuals using Gaussian mixtures.
Implicit Mapping with DNN
A tutorial for representing maps using DNN
Lie Theory for State Estimation in Robotics
A tutorial for Lie theory used in state estimation of robotics.
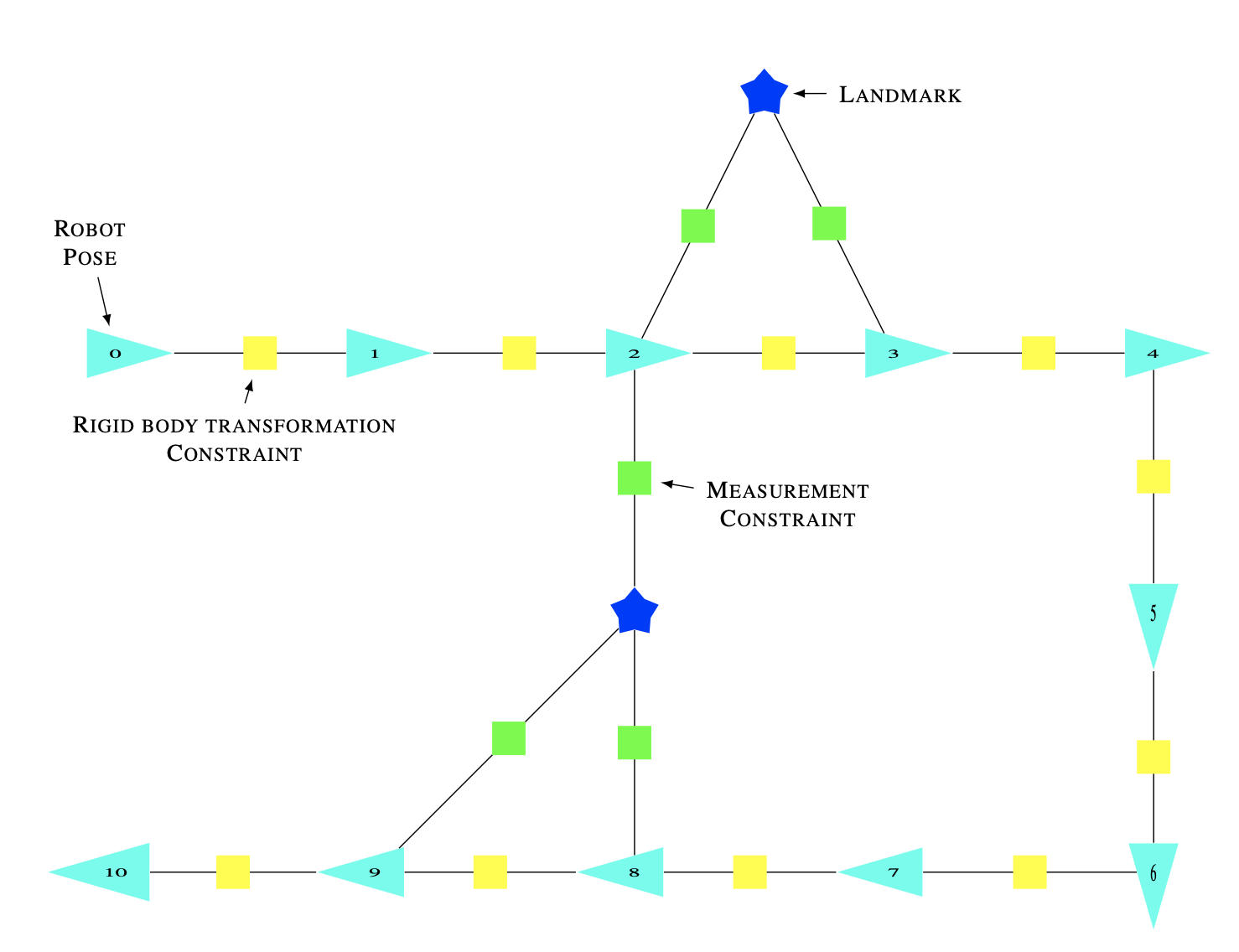
Factor Graph
Factor graph is a nice representation for optimization problems. It allow us to specify a joint density as a product of factors. It can be used to specify any function $\Phi(X)$ over a set of variables $X$, not just probability densities, though in SLAM, we normally use Gaussian distribution as the factor function.
Inertial Navigation System
A tutorial for building INS using IMU.
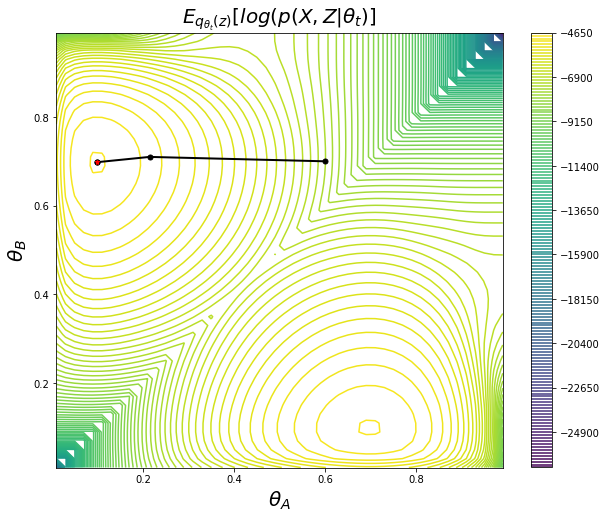
Expectation Maximization
Expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables.
Machine Learning Notes
This is a collection of machine learning study notes.
Robots, Robots, Everywhere!
On the ground, in the air, robots, robots, everywhere! Up in space, beneath the seas, robots make discoveries.